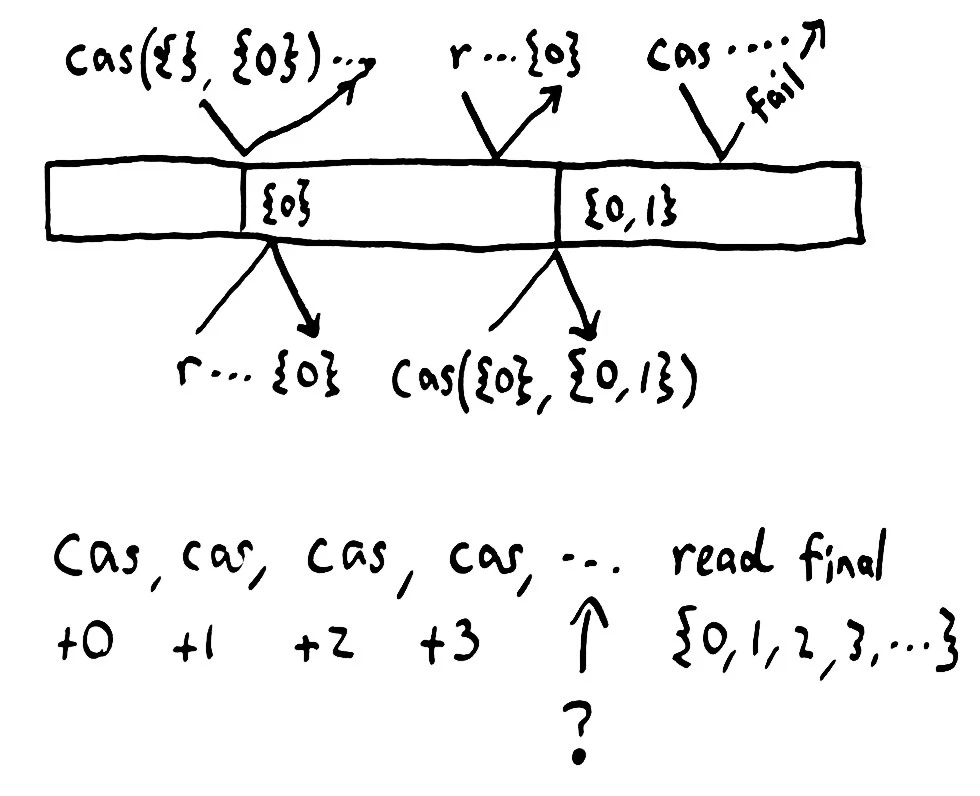
Update, 2018-08-24: For a more complete, formal discussion of consistency models, see jepsen.io.
Network partitions are going to happen. Switches, NICs, host hardware, operating systems, disks, virtualization layers, and language runtimes, not to mention program semantics themselves, all conspire to delay, drop, duplicate, or reorder our messages. In an uncertain world, we want our software to maintain some sense of intuitive correctness.
Well, obviously we want intuitive correctness. Do The Right Thing(TM)! But what exactly is the right thing? How might we describe it? In this essay, we’ll take a tour of some “strong” consistency models, and see how they fit together.
Previously: Logistics
Until this point in the book, we’ve dealt primarily in specific details: what an expression is, how math works, which functions apply to different data structures, and where code lives. But programming, like speaking a language, painting landscapes, or designing turbines, is about more than the nuts and bolts of the trade. It’s knowing how to combine those parts into a cohesive whole–and this is a skill which is difficult to describe formally. In this part of the book, I’d like to work with you on an integrative tour of one particular problem: modeling a rocket in flight.
We’re going to reinforce our concrete knowledge of the standard library by using maps, sequences, and math functions together. At the same time, we’re going to practice how to represent a complex system; decomposing a problem into smaller parts, naming functions and variables, and writing tests.
Previously, we covered state and mutability.
Up until now, we’ve been programming primarily at the REPL. However, the REPL is a limited tool. While it lets us explore a problem interactively, that interactivity comes at a cost: changing an expression requires retyping the entire thing, editing multi-line expressions is awkward, and our work vanishes when we restart the REPL–so we can’t share our programs with others, or run them again later. Moreover, programs in the REPL are hard to organize. To solve large problems, we need a way of writing programs durably–so they can be read and evaluated later.
In addition to the code itself, we often want to store ancillary information. Tests verify the correctness of the program. Resources like precomputed databases, lookup tables, images, and text files provide other data the program needs to run. There may be documentation: instructions for how to use and understand the software. A program may also depend on code from other programs, which we call libraries, packages, or dependencies. In Clojure, we have a standardized way to bind together all these parts into a single directory, called a project.
mrb_bk brought up this wonderful quote today.
What good are impossibility results, anyway? They don’t seem very useful at first, since they don’t allow computers to do anything they couldn’t previously.
Most obviously, impossibility results tell you when you should stop trying to devise or improve an algorithm. This information can be useful both for theoretical research and for systems development work.
It is probably true that most systems developers, even when confronted with the proved impossibility of what they’re trying to do, will still keep trying to do it. This doesn’t necessarily mean that they are obstinate, but rather that they have some flexibility in their goals. E.g., if they can’t accomplish something absolutely, maybe they can settle for a solution that works with “sufficiently high probability”. In such a case, the effect of the impossibility result might be to make a systems developer clarify his/her claims about what the system accomplishes.
–The inimitable Nancy Lynch, in A Hundred Impossibility Proofs for Distributed Computing
A few weeks ago I criticized a proposal by Antirez for a hypothetical linearizable system built on top of Redis WAIT and a strong coordinator. I showed that the coordinator he suggested was physically impossible to build, and that anybody who tried to actually implement that design would run into serious problems. I demonstrated those problems (and additional implementation-specific issues) in an experiment on Redis’ unstable branch.
Antirez’ principal objections, as I understand them, are:
- Some readers mistakenly assumed that the system I discussed was a proposal for Redis Cluster.
- I showed that the proposal was physically impossible, but didn’t address its safety if it were possible.
- The impossible parts of the proposed system could be implemented in a real asynchronous network by layering in additional constraints on the leader election process.
In a recent blog post, antirez detailed a new operation in Redis: WAIT. WAIT is proposed as an enhancement to Redis’ replication protocol to reduce the window of data loss in replicated Redis systems; clients can block awaiting acknowledgement of a write to a given number of nodes (or time out if the given threshold is not met). The theory here is that positive acknowledgement of a write to a majority of nodes guarantees that write will be visible in all future states of the system.
As I explained earlier, any asynchronously replicated system with primary-secondary failover allows data loss. Optional synchronous replication, antirez proposes, should make it possible for Redis to provide strong consistency for those operations.
WAIT means that if you run three nodes A, B, C where every node contains a Sentinel instance and a Redis instance, and you “WAIT 1” after every operation to reach the majority of slaves, you get a consistent system.
WAIT can be also used, by improving the failover procedure, in order to have a strong consistent system (no writes to the older master from the point the failure detection is positive, to the end of the failover when the configuration is updated, or alternative, disconnect the majority of slaves you can reach during the failure detection so that every write will fail during this time).
Previously: Macros.
Most programs encompass change. People grow up, leave town, fall in love, and take new names. Engines burn through fuel while their parts wear out, and new ones are swapped in. Forests burn down and their logs become nurseries for new trees. Despite these changes, we say “She’s still Nguyen”, “That’s my motorcycle”, “The same woods I hiked through as a child.”
Identity is a skein we lay across the world of immutable facts; a single entity which encompasses change. In programming, identities unify different values over time. Identity types are mutable references to immutable values.
In Chapter 1, I asserted that the grammar of Lisp is uniform: every expression is a list, beginning with a verb, and followed by some arguments. Evaluation proceeds from left to right, and every element of the list must be evaluated before evaluating the list itself. Yet we just saw, at the end of Sequences, an expression which seemed to violate these rules.
Clearly, this is not the whole story.
Macroexpansion
In Chapter 3, we discovered functions as a way to abstract expressions; to rephrase a particular computation with some parts missing. We used functions to transform a single value. But what if we want to apply a function to more than one value at once? What about sequences?
For example, we know that (inc 2) increments the number 2. What if we wanted to increment every number in the vector [1 2 3], producing [2 3 4]?
user=> (inc [1 2 3])
ClassCastException clojure.lang.PersistentVector cannot be cast to java.lang.Number clojure.lang.Numbers.inc (Numbers.java:110)
We left off last chapter with a question: what are verbs, anyway? When you evaluate (type :mary-poppins), what really happens?
user=> (type :mary-poppins)
clojure.lang.Keyword
To understand how type works, we’ll need several new ideas. First, we’ll expand on the notion of symbols as references to other values. Then we’ll learn about functions: Clojure’s verbs. Finally, we’ll use the Var system to explore and change the definitions of those functions.
We’ve learned the basics of Clojure’s syntax and evaluation model. Now we’ll take a tour of the basic nouns in the language.
Types
We’ve seen a few different values already–for instance, nil, true, false, 1, 2.34, and "meow". Clearly all these things are different values, but some of them seem more alike than others.
This guide aims to introduce newcomers and experienced programmers alike to the beauty of functional programming, starting with the simplest building blocks of software. You’ll need a computer, basic proficiency in the command line, a text editor, and an internet connection. By the end of this series, you’ll have a thorough command of the Clojure programming language.
Who is this guide for?
Science, technology, engineering, and mathematics are deeply rewarding fields, yet few women enter STEM as a career path. Still more are discouraged by a culture which repeatedly asserts that women lack the analytic aptitude for writing software, that they are not driven enough to be successful scientists, that it’s not cool to pursue a passion for structural engineering. Those few with the talent, encouragement, and persistence to break in to science and tech are discouraged by persistent sexism in practice: the old boy’s club of tenure, being passed over for promotions, isolation from peers, and flat-out assault. This landscape sucks. I want to help change it.